|
|
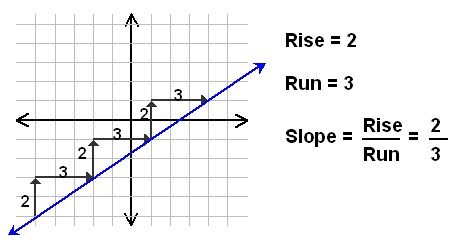
Estimated Pace for this section: 1 hour Required Equipment: Training Manual (Click to download Word Document) Training Page: <Previous | 1 | 2 | 3 | 4 | Next > Training Part 2 Now that you've had a chance to explore slope and develop your own definition for it, it's time to take a look at one of the official definitions. Follow the instructions below and be sure to keep filling in your training manual as you go. One way of defining slope is that it is equal to "rise over run". To find the slope simply find 2 points on the line and measure the vertical distance between them (rise), the horzontal distance (run), and divide the two. The picture below shows an example of this.
To get a better idea of slope as "rise over run" try the 6 examples in the applet below. Try to find the slope of each example by yourself, then look at the solution. After you have completed these try the two examples found in your training manual.
You may have noticed that all of the "runs" in the examples were positive. It doesn't matter if a negative on a fraction is on top or in front, it is still the same value. For example, -1/3 = 1/-3 = -(1/3). It is easiest to just keep any negatives on the top. Now that you are comfortable with slope as "rise over run" we will look at the equation used to find slope. |