Uncertainty Propagation: Numerous time-varying objects, like the trajectory of a satellite orbiting the earth or the fluctuating stock price, can be approximately described by mathematical models. However, no models are perfect, and our knowledge (like the position and velocity obtained from the sensors or the demand and supply information on the market) is incomplete and corrupted by random noise. Consequently, the status of the object can never be predicted exactly but is rather captured by a time-varying probability density function (PDF) satisfying the Fokker-Planck Equation (FPE). Thus a better prediction is possible if we find the status PDF by solving the corresponding FPE, which is the main concern of our research.
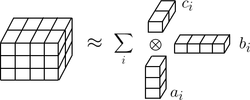
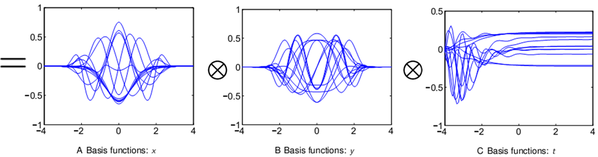
As the number of variables (called dimensionality) of the status increases, due to the "curse of dimensionality", the solution task becomes challenging even when supercomputers are used. Our research is to develop novel numerical methods for this problem merely requiring computational power of a regular personal computer. The idea is to discretize the FPE by Chebyshev spectral differentiation and then approximate its transient solution in a single CANDECOMP/PARAFAC Decomposition (CPD) form, where all the space dimensions and time domain are decoupled from each other, transforming an expensive high dimensional operator into a series of simple one dimensional operators. An illustration of CPD of a given third order tensor is provided by
As the number of variables (called dimensionality) of the status increases, due to the "curse of dimensionality", the solution task becomes challenging even when supercomputers are used. Our research is to develop novel numerical methods for this problem merely requiring computational power of a regular personal computer. The idea is to discretize the FPE by Chebyshev spectral differentiation and then approximate its transient solution in a single CANDECOMP/PARAFAC Decomposition (CPD) form, where all the space dimensions and time domain are decoupled from each other, transforming an expensive high dimensional operator into a series of simple one dimensional operators. An illustration of CPD of a given third order tensor is provided by
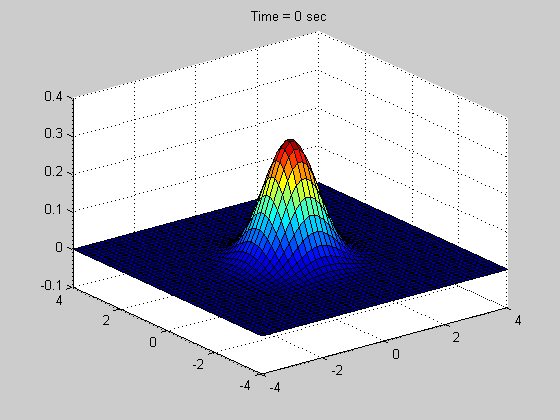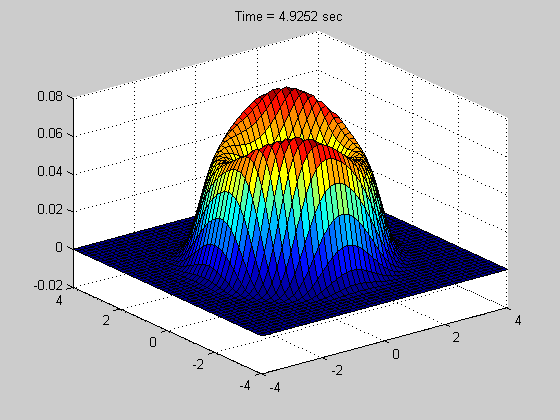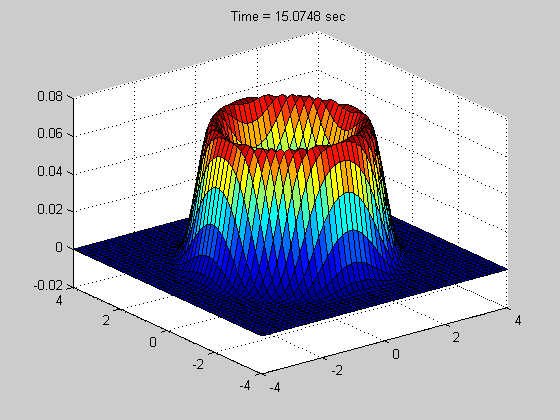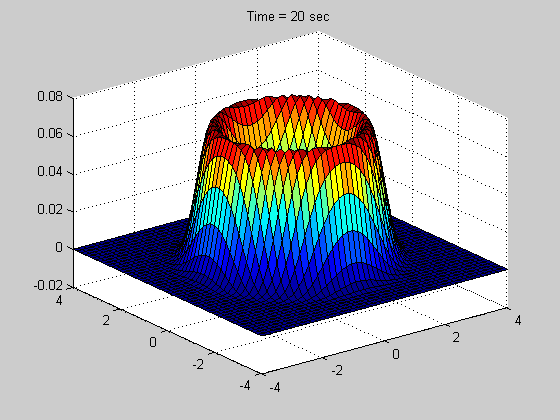
Below is a simple example showing what a CPD representation looks like for a 2D transient solution to a FPE using our method:
So far, we are able to solve a 14D transient FPE on a regular personal computer using merely 24060 degrees of freedom (DOF), while a corresponding DOF in the order of 1e26 is expected if the traditional Finite Element/Difference Method is used.
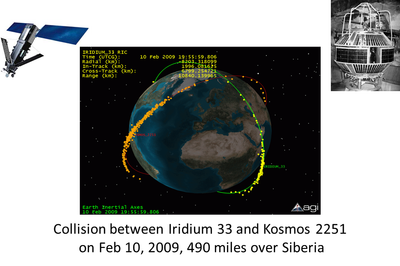
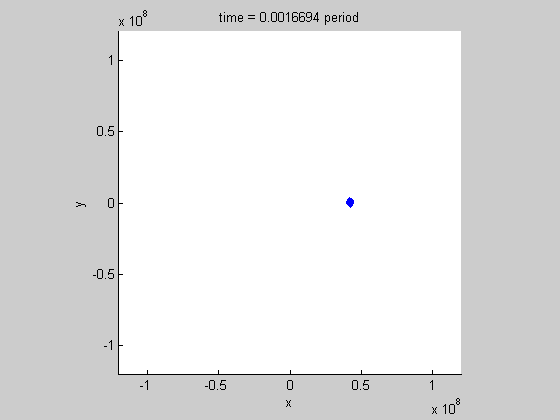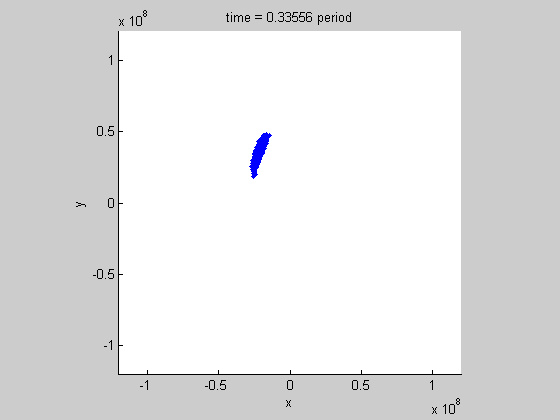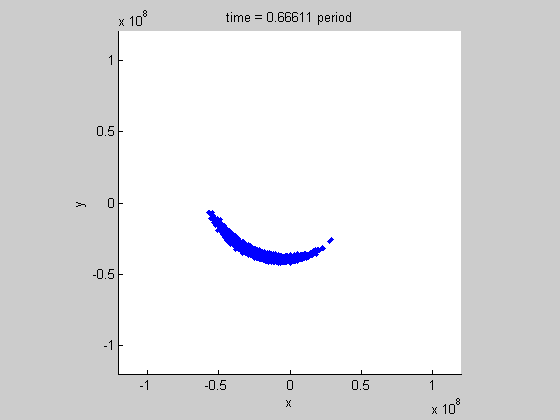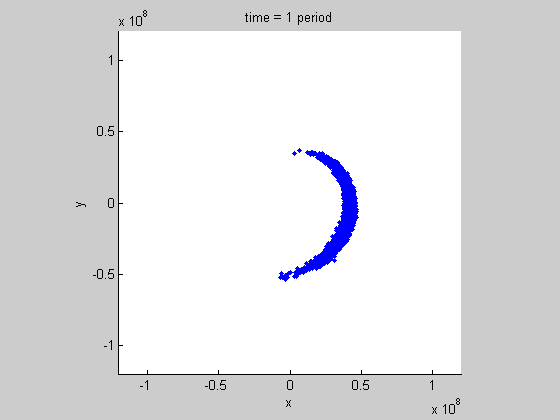
Our research has wide applications such as the space situational awareness (SSA) for the uncertainty propagation in orbits of resident space objects:
Our research has wide applications such as the space situational awareness (SSA) for the uncertainty propagation in orbits of resident space objects:
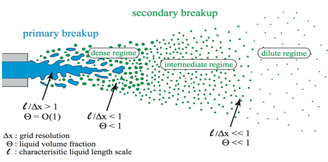
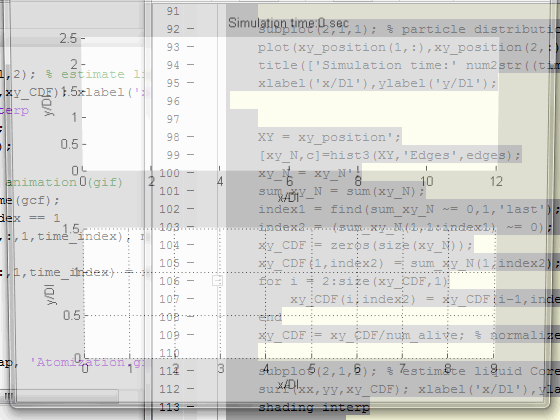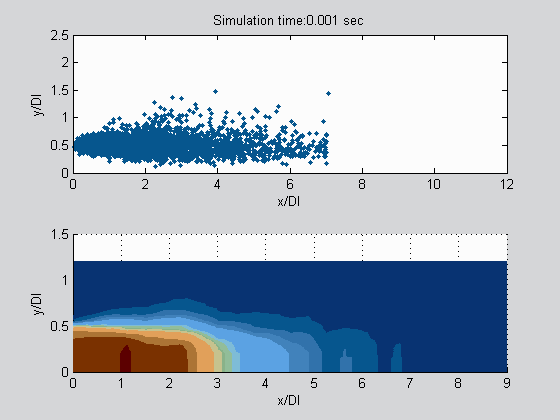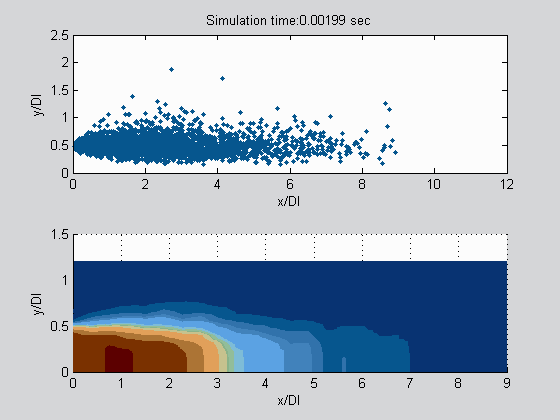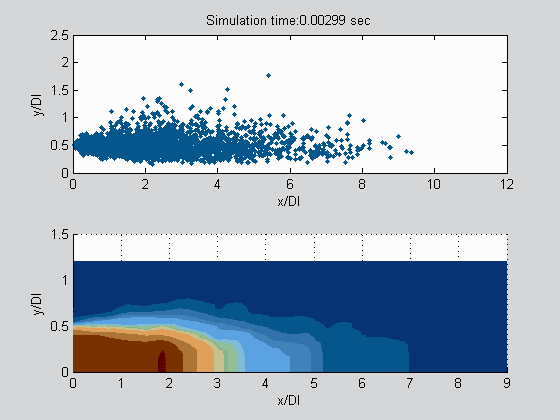
and the stochastic modeling of subcritical primary atomization in liquid rocket engines:
Our research is supported by major funding agencies including: