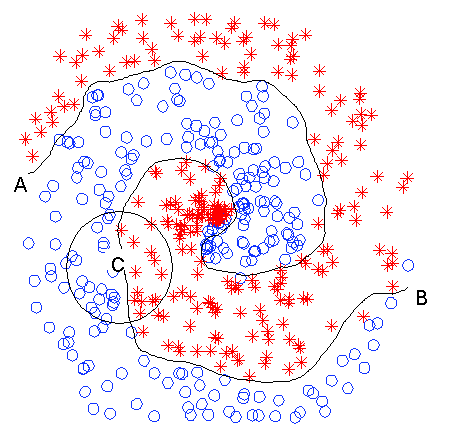
Here is the basic idea of the proposed algorithm. The above is the well-known Fermat spiral problem. Image you were an ant (I know you are not) traveling from point A to point B. If your step size is sufficiently small, after you finish the journey, you would not notice that you have made any turn. Instead, you feel that you always move forward along a straight line (you would have the same feeling when traveling along the world, and this is exactly where the hypothesis of the Flat Earth came). Although the Flat Earth Theory was eventually proven ridiculously wrong, an important implication is that any given complex problem can be more easily, yet accurately enough, analyzed by parsing it into a set of locally linear ones. This idea is behind many important algorithms (e.g., Fourier transform and integral). The proposed algorithm follows the same idea. It first decomposes an arbitrarily complex nonlinear problem into a set of locally linear ones through local learning, and then learns feature relevance globally within the large margin framework. For this reason, the algorithm is called Logo (fit locally and think globally). The algorithm does not make any assumption about the underlying data distribution and is capable of processing many thousands of features within minutes on a personal computer while maintaining a very high accuracy that is nearly insensitive to a growing number of irrelevant features. In one simulation study, our algorithm achieves a close-to-optimal solution even when the spiral data contains one million irrelevant features.

o Y. Sun, S. Todorovic, and S. Goodison, Local Learning Based Feature Selection for High Dimensional Data Analysis, IEEE Trans. on Pattern Analysis and Machine Intelligence, vol. 32, no. 9, pp. 1610-1626, September 2010.

o Supplementary data

o Matlab code

o The paper is featured as a Spotlight Paper in the 2010 September issue of the TPAMI journal.