

60 p term paper
English Linguistics
June 3, 1996
author: Jonas Gustavsson
supervisor: Magnus Ljung
English Department Stockholm University

HTML comments: As you probably will soon notice, dear reader, we are still experiencing some formatting problems. Some tables and figures are not yet fully functional. For readers nourinshing an undisputable ache for these commodities, I sincerely recommend the Microsoft Word-version available on the referring page. The HTML-version will of course get updated, hopefully before the end of humankind.
Acquaintance, which is an n-gram based method for topic and language determination of texts which require no prepared database or preconditioned texts is examined. An implementation of the method which is slightly different from the one proposed by Marc Damashek is described. This implementation is then used to separate English texts from Swedish texts in a collection and to cluster the English texts according to their topics. The possibility to use Acquaintance when having to select one translation out of several alternatives in machine translation is discussed. The method is, however, found to have several severe drawbacks, reducing its versatility.
As the world enters the information age, unprecedented amounts of information become available in electronic form to many people in the developed countries of the world. To make use of this wealth of information, it is necessary to find and collect only those pieces of information which are relevant at the moment. This task requires the texts to be categorized, so that the language they are written in and the subject they deal with can be easily determined. This can of course be done by the writers of the texts, but as different writers would characterize the same text in different ways, a coherent method of categorization which can be used on all texts is needed. Several methods doing this have been developed; most of them based on the topic words of the texts. To find these topic words, e g linguistics, language, pronunciation and syntax in a texts on linguistics, it is necessary to discard all uninformative words that dominate any text, e g the, of, that, a etc. The words to be removed are collected in a so called stop list together with common, topic invariant affixes like un-, -ed and -s. Unfortunately, if we want to collect the texts not dealing just with linguistics in general, but only those texts dealing with the social variations of language, more words, e g language and syntax must be added to the stop list. Topic words making these texts stand apart from other texts, including those dealing with linguistics in general, may be sociolinguistics, stratification and dialect. Hence a specific stop list must be built for every topic area which is to be searched for. In this text I will present the method called Acquaintance, which offers a way around these problems. Acquaintance uses not words, but so called n-grams, i e strings of n consecutive characters ('th_a' is an example of a 4-gram, since spaces are also counted). I have used '_' for space in this paper for clarity. The great advantage of Acquaintance is that the equivalent of stop lists can be set up automatically, using a mathematical algorithm on a computer instead of having someone thinking out which words should be on the stop list when looking for texts dealing with a certain topic.
Knowing the subject matter of a text is not only useful when categorizing large collections of texts, but also when disambiguating certain words as a step in the translation of a text. Most words can be disambiguated as a part of the normal analysis of a sentence; the translation of the word mean can be determined from which words it occur together with and its function in the sentence: verb-> 'to represent', adjective-> 'unkind' or 'unwilling to share' and noun-> 'average value' (The word mean is of course more complex than this, but that is another story). There are, however, words for which a translation cannot be chosen only considering the sentence they are in, e g That looks like a good joint. In this sentence, joint could mean 'marijuana cigarette', 'connection' (e g between pipes in a conversation between plumbers), 'bar' or 'piece of meat'. What it means in the sentence in question, and hence which translation should be chosen, must be determined from the rest of the text. If there are a lot of terms dealing with narcotics in the rest of the text, joint probably mean 'marijuana cigarette' and if the text contains a lot of words (or n-grams resulting from words) like pipe, wrench and fitting, it probably means 'connection between pipes'. In cases like this, it would hence be useful to know the topic of a text (or part of a text1) in order to determine a suitable translation.
In the first part of this report, I will present the Acquaintance method and show how it can be implemented in the form of a computer program written in the C++ programming language. My implementation differs from that of Marc Damashek (1995) on a few points, as will be shown in section 5.2 below. I intend to see how well it performs on language and topic determination tasks and how the method could be developed to improve its performance.
In the second part of the report, I use the method to examine how the sense of the test word workers is related to the topic matter of the texts it occur in according to Acquaintance. I have chosen this word because it spans a wide range of meanings ranging from 'scholars' to 'labourers' via 'employed people in general', so that it can be determined how good a ”resolution” Acquaintance offers and whether it is good enough to be a useful tool in machine translation (to languages that tend to make a greater distinction between different kinds of employees).
In selecting these texts, I wanted clear cases of workers meaning "manual labour" and workers meaning "highly trained professionals" as well as intermediate cases where the interpretation is more uncertain. I did, however, take away all social workers, because social worker may be considered as a lexical item on its own, and the purpose of this part of the study is to see whether Acquaintance can help machine translation systems solve unclear cases. One can, however, not demand that Acquaintance solves cases as uncertain as in ifw-const.txt, where even a human translator would be uncertain which translation to choose.
In this section I will show how a text is analysed using the Acquaintance method as it was presented by Marc Damashek in his article 'Gauging Similarity with n-grams: Language-Independent Categorization of Text' (Science 10 Feb. 1995, p 843ff). The method I have used differs a little from the description in this section. To see how it differs and why I have chosen to change it, see section 5.2.
In order to get rid of a lot of 'junk' text and make n-grams like '_The_', '_the_', '.The_' and '_THE_' be considered as the same n-gram, the text can be preconditioned. Damashek transforms the text so that it only contains the capital English characters 'A'-'Z' and space '_'.
The n-grams, which are sequences of n consecutive characters, are copied out of the text using a window of n characters' length, which is moved over the text one character forward at a time. See figure 5-1.

Figure 5-1. The n-grams are extracted from the text.
Every possible n-gram is given a number, a so called hashkey. This could for example be done like this: 'AAAAA'=0, 'AAAAB'=1, 'AAAAC'=2,..., 'AAABA'=27, 'AAABB'=28, ..., 'AABAA'=729 and so on. How the n-grams are numbered is not important, as long as each instance of a certain n-gram, e g 'A_OF_', is always given the same number, and that two different n-grams are always assigned different numbers. Using this numbering system, some n-grams are assigned large numbers, e g '_____'=14,348,906 in this system.
The hashtable is a list which is used to keep track of how many times each n-gram has been found in the text being studied. Every time an n-gram is picked, the element of the hashtable with the number given to the n-gram is increased by one. See figure 5-2.
Figure 5-2. An n-gram is placed in the hashtable.It is, however, very inconvenient to have hashtables of more than 14 million positions length, so shorter lists are used (Damashek uses 262,144 positions). This means that several different n-grams will be 'stored' at the same position, but since most of the possible n-grams, e g 'AAAAA', 'BBBBB', never occur in normal texts, collisions, where contributions from several different n-grams are added together, are very infrequent and should, according to Damashek, not affect the outcome very much. See figure 5-3. Note that the size of the hashtable is unaffected by the size of the text being analyzed - a novel will take up as much memory as a leaflet.
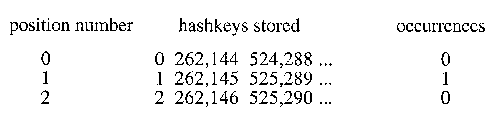
Figure 5-3. How hashkeys are stored in the hashtable.
The hashtables can be treated as vectors3, so called document vectors, in a 262,144-dimensional space which point from the origin to points on a 262,143-dimensional hyperplane4, created through the normalization. Document vectors resulting from similar texts point in almost the same direction. The similarity score between two texts is defined as their scalar product divided by their lengths. A scalar product is calculated through summing up the products of the corresponding elements (i e those resulting from the same n-grams). See figure 5-4 below. This is the same thing as the cosine of the angle between the documents (i e the points on the hyperplane the document vectors point to) seen from the origin. The reason for defining the similarity this way instead of as simply the distance between the points the document vectors point to will be given in section 5.1.8. below. The similarity scores between all pairs of texts will be numbers between 0 and 1, where 1 signify (almost) identical texts and 0 completely dissimilar texts, where there are no n-grams that occur in both texts.
Position Vector/text 1 Vector/text 2 Product
Figure 5-4. Calculation of the scalar product of two vectors.
Since the largest elements of the document vectors correspond to common n-grams produced by words like the, and and of and by common affixes like un- and -tion, which are language more than topic specific, all pairs of texts written in the same language will be given high similarity scores. This means that a threshold value of the similarity score can be used to determine which texts are written in the same language (these text pairs have a similarity score greater than the threshold value) and which texts are written in different languages. The texts scoring a similarity score above the threshold value are grouped (clustered) together in clusters, so that there will be one Swedish, one English, one German and so on, cluster, provided that these languages are represented among the studied texts. The so called centroid of the clusters, i e a point in the middle of the texts, representing a 'typical member' of the cluster, is calculated as the arithmetic mean of the hashtables of the texts in the cluster. Apart from telling which language a text is written in, Acquaintance also offers a quantitative measurement of the similarity of different languages as the similarity scores of the centroids of the language clusters to be compared. Swedish and Norwegian have a much higher similarity score than for example English and Hindu. See figure 3 in Damashek (1995) for a nice example of this comparison of languages.
Normally, the topic of a texts is more interesting than the language in which it is written. To get to the topic of the text, the uninformative n-grams must be removed, just like the uninformative words are discarded by the stop lists in word-based analysis methods. Here this filtering can be performed simply by subtracting the centroid of all texts written in the same language from the members of the cluster. This is equivalent to moving the point-of-view to the centre of the cluster. See figure 5-5. When viewed from that point, the texts in the cluster will be much more spread out than earlier (i e the similarity scores will be lower) and the texts now scoring high similarity scores are those that have more than the language-general n-grams in common and hence share some element of topic. Again a threshold value is used to determine which texts deal with the same subject and these texts are clustered together. Should the relevant cluster still be contain too many texts, the 'zooming-in' procedure can be repeated until the number has been brought down to an acceptable level and the subject matter is defined in sufficient detail. The reason for defining the similarity score as the cosine of the angle between the documents seen from the current point of view instead of simply the distance between the texts in space, is that the distance between the studied texts will decrease with each zooming in, so that the threshold value would need to be reset after each zooming in.
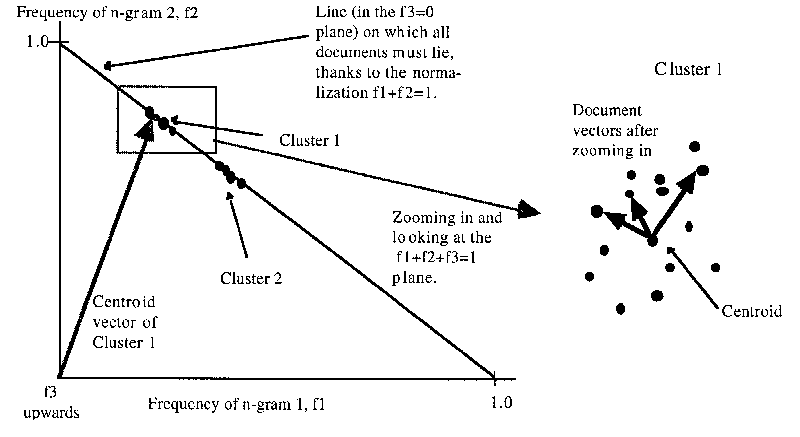
Figure 5-5. Zooming in a language cluster.
In figure 5-5, only three n-grams/dimensions are used, as would be the case in a language with only the letters 'A', 'B' and '_' when analyzing it using 1-grams (i e simply the characters). f1=1, f2=0, f3=0 would then correspond to a text with only 'A's etc. As can be seen in the figure, before the zooming in, all document vectors (only their end-points are shown in the figure for clarity) in a cluster are almost parallel to the centroid vector and each other. This means that the similarity scores between the texts are high, because the angles between the document vectors (hashtables) are small and the cosine of a small angle is close to 1. After the zooming in (note that the cluster then is seen from another angle), the document vectors of the texts in the cluster start from the centroid of the cluster. Then the text will be much more spread out, as seen from the starting point of the document vectors, the angles between the texts greater and hence the similarity scores lower. If two texts still have nearly parallel document vectors, they share more n-grams than those given by the language-related similarity that is represented by the centroid.
Marc Damashek (1995) preconditions the text by converting all characters in it to the English upper case characters 'A'-'Z' and space. How, for example, the special Swedish characters Ā, Ä and ... are converted is not stated. I think this conversion means an unnecessary loss of information when analyzing other languages than English. The n-grams that contain Swedish characters are very strong indicator of that the text is not English, because such n-grams never occur in English text (unlike in this text and the like). Whether one should convert all characters to capitals or not, is a more debatable issue. I have chosen not to do this conversion, but this means that 'mixed' databases that contain both texts in 'natural style', i e both lower and upper case characters as in normal texts, and texts where all characters are in either upper or lower case cannot be analyzed, since the computer does not see any connection between e g 'a' and 'A'. The advantage of distinguishing between upper and lower case characters is that the difference between common nouns and proper names in many languages like English or Swedish is preserved and the difference between nouns and other words in German.
The problem with hashtables is that the results when using them is affected by the number of collisions (n-grams being stored at the same position in the table). Damashek suggests that these collisions are insignificant, because they are so few, but in doing an earlier work on the Acquaintance method, I found that the collisions may seriously affect the efficiency of the method, reducing its ability to discern between similar and different texts even with hashtables filled to just a few percent. The files deposit 4 and 5 that are presented in appendix A are the results of text analysis of the same texts with different hashtable lengths (100,003 and 1,000,003 respectively). As can be seen, the Worst Case Quota (WCQ)2 is reduced drastically when using the smaller hashtable. This means that large hashtables, in which more than say 95% of the elements are zero, must be used. Since this means a serious waste of memory space, using a hashtable of size 1,000,003 just to store the n-grams of a leaflet of a few thousand characters length, a more efficient method of storage must be found. The hashtables may also be developed so that collisions can be handled properly , see Salton (1989, p 192-201) or Knuth (1973, p 503-549). A completely different representation of the hashtables can, however, be chosen as well. The simplest way of doing this is to create a simple list where the occurring n-grams and their frequencies are stored, as is shown in figure 5-6.
n-gram 'hashkey'frequency140.0012120.0022180.0014120.002......Figure 5-6. A (normalized) simple list used to store n-grams and their frequencies.In this way the memory usage is optimized, since no unnecessary zeros are saved. Using this method, the collisions are also completely avoided, since the list is made so long that each n-gram can be assigned an element of its own in which to sort its frequency. The problem with this representation is that when inserting a new n-gram in the sorted list, one must pass through all elements with a lower 'hashkey'. Example: If a text of 10,000 n-grams (and approximately as many characters) distributed among 5,000 different types is to be analyzed. Then the first n-gram found starts off the hitherto empty list. The second n-gram picked out is compared with this first element of the list and placed before it if it has a lower hash key value or hung on after it if it has a higher hashnumber. If the hashnumbers are equal, the number of occurrences of this n-gram is increased by one. As more and more n-grams are inserted into or appended after the list, it will become longer and longer. When the last n-gram is to be inserted, the list will contain 4,999 or 5,000 elements and in order to sort in the last n-gram, it will have to be compared with, on average, 2,500 n-grams. The total number of comparisons needed to set up the list will be about 12.5 million. When using a hashtable, no such comparisons are needed, since the place where the n-gram should be stored is given directly by the hashkey. This large number of comparisons will take some time, even on a quick computer, and for longer texts, the method cannot be used, since the number of computations will tend to grow as the square of the number of n-grams in the text.
Another way of assuring that no collisions occur, is to use a binary tree to store the n-grams and their frequencies. In a binary tree, each element is not just connected to two other elements – the one with the closest lower hashnumber and the one with the closest higher hashnumber, but to three other elements. The purpose of this is to drastically reduce the number of comparisons necessary to sort in a new n-gram among the already found ones. See figure 5-7 for an example of how a binary tree might look.

Figure 5-7. An example of a binary tree.
The lo links point to elements with lower hashnumbers and the hi links to elements with a higher hashnumber.When sorting in a new n-gram in the binary tree, one starts from the top of the tree, at which the first n-gram of the text to be analyzed has been stored. Then what happens depend on how large the hashkey of the n-gram to be inserted is compared with the hashnumber at the top of the tree. If the hashnumbers are equal, the number of occurrences of that hashnumber is increased by one, and a new n-gram to be sorted in is picked up from the text. If the hashnumber of the new n-gram is smaller than the hashnumber of the top element (node), the lo link is followed otherwise, the hi link is followed. Then the comparisons continue at the new nodes and the procedure until a match is found or the end of the tree is reached. If there is no link of the desired kind, a new node is crated for the n-gram to be stored in on that position.
Example: An n-gram with a hashnumber of 1,542 is to be added to the tree in figure 5-7. First, it is compared with the hashnumber 2,342 of the top node and since it is smaller than that number, the lo link is followed. Comparison with the hashnumber of the node found there, 1,232, reveals that the n-gram belongs somewhere down the hi link. Since 1,542>1,321, it is to be sorted into the hi branch of the 1,321 element, but since the hi link of that element does not point to any element, a new element is created below the 1,321 element. The hi link of the 1,321 element will then point to an element with the form: hashnumber: 1,542 occurrences: 1.
The binary tree makes it possible to sort in n-grams without having to compare their hashnumbers with as many other hashnumbers as with the simple list. A binary tree with only 10 'levels' (i e maximum number of necessary caparisons to sort in an n-gram) will house 1,023 different n-grams. More information on binary trees can be found in Knuth (1973, p 167-175).
The binary tree is, as has been presented above, superior to the simple list when in comes to sorting in a new element, and the same goes for the retrieval of a given element, e g the number of occurrences of the n-gram with the hashnumber 1,524 in a text. The binary tree also shares the positive properties i) no more memory space than necessary used, and ii) no collisions, with the simple list. Unfortunately, it is still slower than the simple hashtable, since a number of comparisons must be made in order to find a certain n-gram or a place to store a new n-gram in.

Table 6-1.
The similarity scores from appendix C rounded off to three decimal places. The lower left half of the table is identical to the upper right half reflected in or rotated about the 1-diagonal. The WCQ2 can be calculated as S(6,11)/S(2,9)=0.57.Since the WCQ is less than 1, so the method succeeds in dividing the texts into two primary clusters, one of the Swedish texts and one with the English texts only because dissimilar texts like 6 and 11, which are both written in English, both score above the threshold when compared with bridging texts like number 10. Were it not for these texts, 6 and 11 would be judged to be written in different languages, because they are so different.
Having divided the texts among these two clusters and let the user name them, the computer wants to know which cluster to have a closer look at. Cluster 2, the English cluster, is chosen and the centroid of this cluster is subtracted from all texts/document vectors in this cluster. The Swedish texts are left out of the subsequent analysis.
Having done this zooming in, another clustering is performed. This time the computer identifies three clusters within the English cluster: cluster a (no 3) with the texts pg3.txt, lmrisk.txt, cap16.txt, child.txt, ifww-const.txt and hci.txt, cluster b (no 4) with carb.txt and dept_info.txt and cluster FieldStaffInformation (no 5) which only contains the text feature5.txt.
This result is very surprising. One would have expected the texts 3-7 to form one cluster and 8-11 to form another, since the former texts deal with working conditions and manual labour, while the latter texts are texts about trained professionals. It is possible to accept that the texts 9, 10 and 11 get split up on two clusters, after all the centroids of these clusters have a similarity score with one another above the threshold level. What seems more astonishing is that hci.txt, a text dealing with human-computer interaction, is included in cluster a together with texts on subjects that seem very unrelated. This would make it impossible to use the clustering to determine what type of person is being referred to by the term worker.
Since it is the largest cluster, number 3 (a) is then selected for a closer analysis. After the zoom-in, the only pair of texts to score a similarity score above the threshold level are pg3.txt and lmrisk.txt. All other texts are put in separate clusters.
That the two texts to be grouped together at this level are pg3.txt and lmrisk.txt, is not very surprising, since they both deal with working conditions. One can also note that the text child.txt that deals with child labour in Bangladesh has something in common with the texts in this cluster and score a similarity score of 0.065 when compared with pg3.txt, i e just below the chosen threshold level. Since the threshold level of 0.07 is chosen empirically, and the only demand on it is that it must be in the range 0. 039-c 0.2 for the language determination is to work properly, it can be lowered so that child.txt is included in the cluster, should that be desired.
It is equally disappointing that Acquaintance does not seem to be able to offer any help when it comes to choosing the right translation of a word, since it cannot accurately determine the subject area of a text. This problem seems to occur not just for borderline cases, in which even a human translator would have a hard time choosing the right translation of, but as exemplified by the clustering of the text hci.txt.
A closer look at the text carb.txt may provide an explanation to some of these problems. The text is found to feature massive indentation in the form of a large number of spaces. The spaces will create a great number of n-grams, which is not found in any other texts, and hence will make carb.txt stand out from the other texts in the analysis. These problems can probably be solved using more extensive preconditioning, so that similar texts acquired from sources using different text formats (eg spaces instead of tabulators) look more alike to the computer before the analysis commences.
The advantage of Acquaintance is that it does not, unlike other methods for topic determination, need a large database like word and affix stoplists. Unfortunately, it is not very quick in its current form, using binary trees. I would like to examine whether a more advanced hashtable, where collisions are handled properly, gives shorter execution times than the current implementation. The test I have described in this paper with eleven texts with lengths varying from 2,700 to 24,000 characters, requires 90 minutes of CPU-time on a SUN minicomputer, which must be considered absurd. When examining large collections of texts, it is impossible to compare all possible pairs of texts. Instead, one can pick out a collection of texts and cluster them first and then only compare the rest of the texts with the centroids of these clusters.
Another possible way of speeding up the analyze process, is to use fewer n-grams in the analysis. When categorizing books, one could for example confine the analysis to an abstract. Another, drastic, approach has been proposed by William Cavner (1995) – he suggests that language-specific stop lists should be used for reducing the number of stored n-grams and extracting topic-specific information. Both these approaches does, however, limit the usefulness of Acquaintance because they need either databases to be set up or the text to be analyzed to be preconditioned.
2. Worst Case Quota (WCQ) = (the lowest similarity score for a pair of texts written in the same language)/(the highest similarity score for a pair of texts written in different languages) WCQ is a measurement of the certainty with which Acquaintance can separate texts written in different languages from each other and cluster them together in one cluster per language. WCQ must be greater than 1 for Acquaintance to stand a chance to discern between languages, and preferably it should be as large as possible, making the use a wide range of threshold values possible. WCQ is lowered by the collisions in hashtables and the 'true' WCQ (without collisions) decreases when texts that are very dissimilar to one another, but still written in the same language (e g from different historical periods) are introduced.
3. A vector is a list of numbers, often written like (2,6,1). Vectors of the same length (i e number of components or dimensions) can be added together by adding the corresponding components in two vectors, e g (1,3,4)+(2,1,8)=(3,4,12). Vectors of different lengths cannot be added.
4. In three dimensions, like in figure 5-5, a hyperplane would be a common two-dimensional plane, cutting through the paper along the f1+f2=1 normalization line and the f3 axis at 1.
Damashek, Marc, 1995, `Gauging Similarity with n-Grams: Language-Independent Categorization of Text', Science 267 (10 Feb. 1995), p 843-848.
Knuth, D E, 1973, Sorting and Searching, volume 3 of The Art of Computer Programming, Reading: Addison-Wesley.
Salton, Gerard, 1989, Automatic Text Processing, Reading: Addison-Wesley
B. The program used in doing the analysis of this paper (Copyrighted).
acquaint3.cc the main program
cluster.cc & .hh used to store the clustered documents. In the start of the analysis, all texts belong to cluster 0 and then new clusters are created through the Acquaintance-analysis.
matrix.cc & .hh a simple matrix class used to store the similarity scores between different hashtab:s in
hashtab.cc & .hh (despite their names) used to store the texts in the form of a link to their binary trees and names
simplelist.cc & .hh a simple list used for storing the n-grams temporarily as they are picked out of their texts
bintree.cc & .hh the binary tree in which the n-grams are stored
longint.cc & .hh holds the n-grams' hashkeys, which are to large to be stored using the simple numerical formats of the computer
C. utfil2, the output (and input) produced when executing the program.

Jonas Gustavsson (English homepage)
Jonas Gustavsson (Swedish homepage)