Separation of Instruments
Steven T. Wright and Justin C. Zito
EEL 6586 – Dr. John G. Harris
April 25, 2008
INTRODUCTION
The goal for our project is to
separate a single channel recording of two musical instruments into two
individual tracks, each containing a single instrument. We created a recording of a trombone playing
along with a drummer. The instruments
chosen for this experiment were inspired by our individual passion for the
trombone and drums, respectively. Our
recording is a fifteen second long rendition of the tune “We Got the Funk,”
originally performed by Positive Force
in 1979. Essentially we are converting
an ensemble track into two solo tracks.
Figure 1: Neal Smith of Alice Cooper [1]; click
on the image to hear our original recording
Motivation for our design comes from
several areas. It can be used
educationally, for example, in the case where a student would like to learn to
play a song. The student could extract
the track for the instrument of choice, allowing them to focus on learning the
part of interest. It is difficult to
listen to music and hear only one instrument, and even more difficult to learn
from a noisy recording vs. a clean track of the instrument of interest.
It can also be useful for a musician
to listen to a recording of their performance for self improvement. Tempo, tone, and dynamics may vary in playing
alone vs. playing along with other musicians.
A way to separate the tracks for individual playback would allow the
musician to better analyze their own part for adjustments.
Recording individual tracks for each
instrument or voice in a music piece is critical in the production of
commercial audio. The tracks can be
tweaked individually, allowing volume control, reverberation, warping and many
other audio effects for each channel.
Equipment such as a four-channel mixer is necessary for multi-channel
input recording. This equipment,
however, is not cheap. Our method
eliminates the need for such equipment while still generating two instrumental
tracks for individual manipulation.
The microphone used in recording is
a standard desktop computer microphone.
These are unidirectional and help to reduce background noise. The music is not played directly into the
mic, though it is appropriately loud enough such that the mic records a rather
clean audible signal. Ideally, one would
use a condenser microphone in a noise free recording studio for optimal
SNR. This requires access to rather
expensive equipment, and is impractical for most. We use the desktop microphone in conjunction
with Window’s sound recording program to save our file for processing with
MATLAB software. The recordings are
saved as 16 bit, PCM wav files so that they are compatible with MATLAB version
7.0.
APPROACHES
CONSIDERED
Drum Extraction and
Resynthesis
The
following method is developed in [2].
1.
Pre-processing – extract a monaural
signal with enhanced rhythmic content from a stereo signal
2.
Filter bank – decompose signal into
eight non-overlapping sub-bands
3.
Noise subspace projection – extract
the stochastic portion of each sub-band signal
4.
Drum event detection – create
extraction masks for bass drums, snare and cymbals
5.
Drum resynthesis – create weights
from the masks and weight the stochastic signals in each sub-band
Noise subspace projection: based on
the Exponentially Damped Sinusoidal model.
The signal can be decomposed into a harmonic component, modeled as a sum
of sinusoids with an exponential decay, and a noise component defined as the
difference between the original signal and the harmonic component.
Independent
Component Analysis (ICA)
We followed a method proposed by
Jang and Lee [3] that applies to single channel observations. In this case, blind signal separation is performed
upon a single-channel recording. It
begins by assuming the observed signal is the summation of 2 independent source signals.
A fixed-length segment drawn from a
time-varying signal is expressed as a linear superposition of basis
functions. The algorithm is trained with
a priori sets of time-domain basis
functions that encode the sources in a statistically efficient manner. These basis functions are essentially
training sets created from clean recordings of the instruments or voices. They are used in place of the second channel
in our underdetermined system. Some
examples of basis filters include discrete cosine transforms (DCT), Gabor
wavelets, ICA and PCA.
The ICA learning algorithm searches
for a linear transformation Wi
that makes the components as statistically independent as possible.
The learning algorithm uses a
maximum likelihood approach, given the observed channel and the basis
functions. The learned basis filters
maximize the likelihood of the given data.
The
algorithm makes use of the
The major
advantage over the other time domain filtering techniques is that ICA filters
utilize higher order statistics, such that there is no longer an orthogonality
constraint on the subspaces [3]. Thus,
the basis functions obtained by the ICA algorithm are not required to be
independently orthogonal. This algorithm
is most successful at separating voice from jazz music. Jazz music typically includes bass, drums and
some brass instruments.
OUR
APPROACH
We decided
on an approach that targets the sustained tones of the trombone. Early attempts with bandpass filters had
problems with windowing leakages. We
realized that the trombone frequencies are set for each octave. Knowing this we decided to target these
specific notes with conventional filtering methods. The technique that proved most successful was
using combined IIR comb filters to remove the trombone. The comb filters remove all harmonics of the
trombone while leaving the wideband transient drum beats and cymbals
uncorrupted. The combination of comb
filtering with emphasis on high frequency content led to our final drum
track.
The drum
set posed some challenges in source separation, due to the many different
sounds that can be produced by the drummer.
All of the drum components can be represented as transients in the time
domain. The bass or kick drum has the
lowest frequency, then the snare drum, and the hi-hat and crash cymbals reach
the highest frequencies. We needed to
develop a technique that would suppress the trombone but would not interfere
with the snare and bass drum. The
following section presents our results as we progressed through the stages of
our single instrument extraction.
RESULTS
The original recording passes through a myriad of filtering
techniques before generating the final track.
The sound wave for the fifteen second recording is shown for each step
through our progression. Our results
show that we were successful only at separating the drum track from
dual-instrument recording. Extracting
the trombone proved to be more challenging than the drums. We then focused on extracting the drums and
filtering the trombone. Since every
tonal instrument plays the same frequency for a particular note, we can target
and remove these specific frequencies and their harmonics, making it much
easier to extract the transient drum signals.
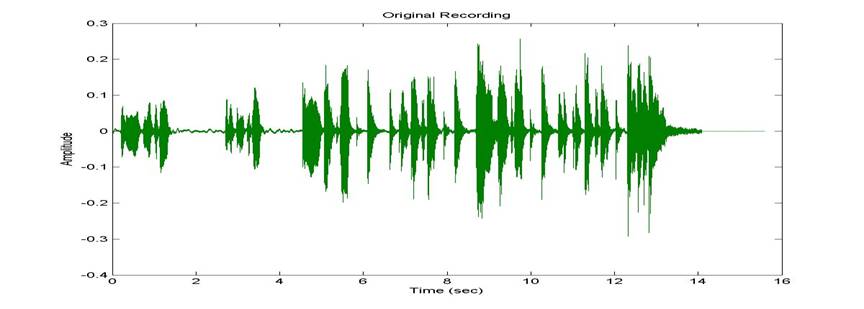
The sound files can be heard by clicking on the corresponding image. The original recording is shown below.
Figure 2: Original recording
The challenges in drum extraction, according to open literature,
often point to the cymbals. The cymbals
have a very sharp impulse followed by a short transient ringing, and encompass
a bandwidth from 300 – 16000 Hz [4]. To
extract the trombone signal, our first step was to filter out the high
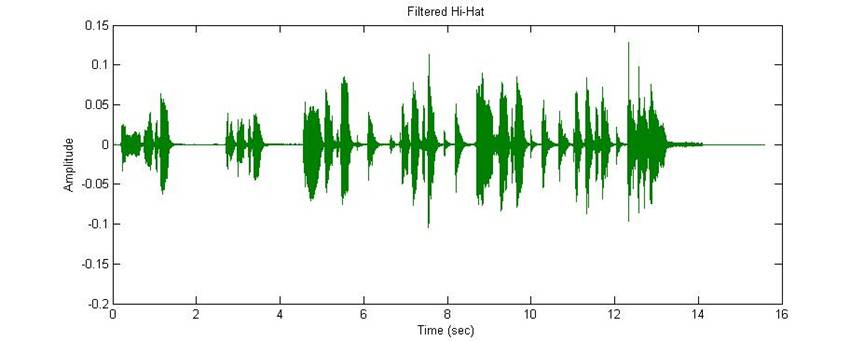
frequency components of the cymbals and hi-hat.
Running our signal through several bandpass filters produced the
following track. The hi-hat component,
which is the constant cymbal tapping throughout the drumming, is well
attenuated. However, the crashing or
ringing of the cymbal is not attenuated and can be heard in both places that it
occurs. This early stage in our progress
was demonstrated in our April 14th presentation.
Figure 3: Filtered hi-hat
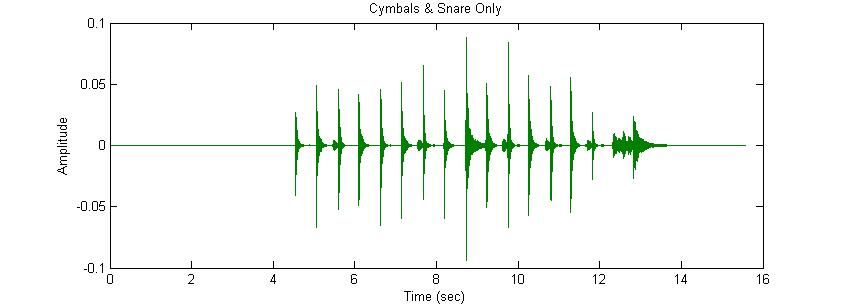
The next breakthrough in our progress occurred when we
changed our focus from the extraction of the trombone to that of the
drums. We realized that it is much more
effective to target the musical frequencies of a range of popular notes played
in music. The trombone is completely
eliminated with more filtering targeting lower frequencies. This allows the extraction of the snare drum
and all cymbals. The drawback here is a
large corresponding attenuation of the bass drum. The snare loses its low end and sounds very
distorted and unnatural. The signal as a
whole looses intensity as well. This
file was also shown in our class presentation.
Figure 4: Cymbals and snare only
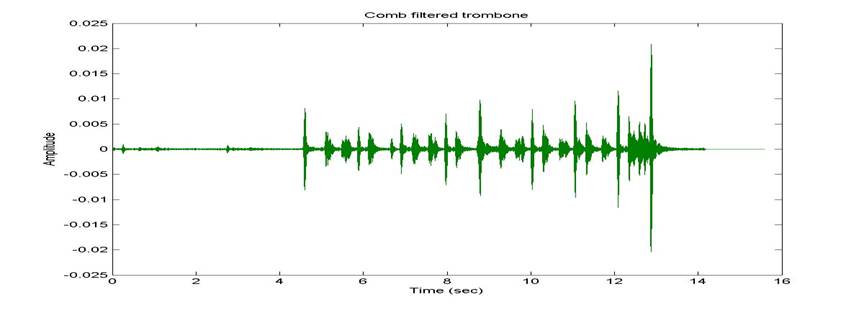
The trombone was filtered most successfully using a bank of
comb filters. Using comb filters, we can
target the specific frequencies for the notes of the trombone and filter them
and their harmonics. We decided to use
one full octave of notes in our filter bank, ranging from 110 to 220 Hz,
corresponding with the 2nd octave range [5]. Filtering over a full octave accounts for all
possible trombone notes played within that range of frequencies. The drawback is obvious; if the notes are
from another octave then they will not be affected at all. If the notes played are within this filtered
range of frequencies, we will generate a single recording of the drum
track. After comb filtering out this
range of frequencies, including their harmonic parts, we recovered a somewhat
robotic sounding drum track. The first
five seconds, where the trombone plays alone, are almost completely
attenuated. You can definitely hear the
effect of filtering the complete second octave of notes in the music
scale. The main benefit in this track is
that the bass drum has been partially recovered from attenuation and
distortion.
Figure 5: Signal after several comb filters applied to
trombone
After several attempts we finally created a track consisting
of the drums only. We filtered specific
instruments and summed several partial signals together. For example, the high frequency components of
the cymbals and snare drum were filtered in one signal and combined with
another signal that was filtered several times for trombone extraction. The bass drum is more audible if you have a
subwoofer.
Figure 6: Final drum track
Compared to the signal in Figure
4, when you could barely, if at all, hear the bass
drum, this is a great improvement. All
of the components of the drums are clearly audible. The quality of the snare drum and cymbals is
much, much improved from earlier attempts.
The combined tracks introduce much less attenuation to the low frequency
components of the drums. The kick drum
sounds appropriately ‘deep,’ and well distinguishable from the snare drum in
quality.
CONCLUSION
In the end we are happy with our
drum track, considering we were merely neophytes in source separation
techniques four weeks ago. There are a
few moments where the trombone can be heard if listening carefully. However, the drums dominate the sound we hear
and have much greater intensity over the trombone. It would be easier to play along with the
final drum track than the original recording for learning purposes. We did not, as we originally desired, create
an individual track for the trombone as well.
More work is needed in creating the individual track for the trombone
(or any tonal instrument), due to the complexity of filtering the drum
components. Our recording consists only
of the two instruments indicated.
Ultimately, the ideal goal is the separation of N instruments into N
individual tracks from a single channel recording. Future developments in our algorithm are
required to separate any two instruments into individual tracks. The algorithm proposed here is a small yet
promising step toward SIMO instrumental source separation with an unlimited
number of sources.
REFERENCES
[1]
“The Worley Gig – Blog Archive – Neal Smith Mirrored
Premier Vintage Drum Set For Sale,” WorldPress 2.2.1, 2007. <www.worleygig.com/blog/archives/004222>
[2]
O. Gillet
and G. Richard, “Extraction and Remixing of Drum Tracks from Polyphonic Music
Signals,” IEEE Workshop on Applications
of Signal Processing to Audio and Acoustics, New Paltz, New York, 2005,
pp. 315-318.
[3]
G. Jang
and T. Lee, “A Maximum Likelihood Approach to Single-channel Source
Separation,” Journal of Machine Learning Research,
vol. 4, pp. 1365-1392, Dec. 2003.
[4]
“T’s
Technical Notes – Frequencies, Frequencies, and More Frequencies,” Terry Downs
Music, 1996. <http://terrydownsmusic.com/technotes/Frequencies/FREQ.HTM>
[5]
“Music Scales – Frequency, Notes,
Octaves, Tuning, Scales, Modes, Pentatonics, Transforms – Yala,” T. Y.
Abdullah, <http://www.geocities.com/SunsetStrip/Underground/2288/4scales.htm>